Softmax函数公式如下，其中yi代表分类i的评分:

$$softmax(y_{i})=\frac{\exp y_{i}}{\sum_{j} \exp y_{j}}$$

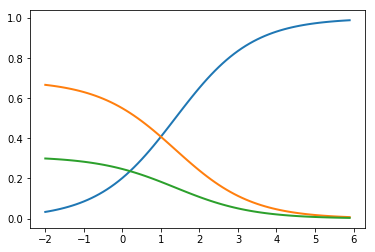
原理是对logistic回归所取得的评分(Score)逐个求对数，然后除以所有评分的对数的总和，可以理解为取评分最高的一个分类。而且Softmax所求得所有分类的概论加起来刚刚好等于1(参加附图，x轴为最有可能分类的评分，蓝色线为最有可能分类的概率)。

我们可以使用Python实现Softmax，而且只需要一行

def softmax(x):
    return np.exp(x)/np.sum(np.exp(x),axis=0)

通过softmax函数，我们就可以使用线性回归进行机器学习的多分类

P.S.可以使用以下代码，复现上图的结果

import matplotlib.pyplot as plt
x = np.arange(-2, 4 , 0.1)
scores = np.vstack([x, 0.4 * x , 0.2 * x])

plt.plot(x, softmax(scores).T, linewidth=2)
plt.show()