什么是数据流分析

数据流分析是一种代码分析方法，可以通过代数方法，对程序中的语义信息进行分析汇总，从而推断出程序在动态执行中变量的定义(Definition) 与使用 (Use) 信息。

  • 在编译器中，通过数据流分析，编译器可以了解变量间的定义和使用关系，从而在编译期间提前计算部分常量传播 (Constant Propagation) 优化，降低程序运行时所需的计算量。
  • 数据流分析也可以协助编译器检查某段代码是否可达 (在动态运行时能不能执行到)，编译器可以结合分析结果，移除部分不可达的代码
  • 在软件开发和测试中，数据流分析作为静态分析方法，在程序不运行的情况下，对变量的声明、赋值、使用进行分析，并形成合理代码的改进建议

什么是基本块

基本块是一段代码，在这段代码中，顺序执行时只能从唯一的入口进入，从唯一的出口离开，代码中没有任何分支（if, else, while, for …) 存在。如下述代码

1
2
3
4
5
6
7
8
int x = 1;
int sum = 0;
while( x <= 100)
{
  sum += x;
  x ++;
}
printf ("%d\n", sum);

其基本块可以划分为：

基本块划分

在编译优化中，我们一般使用中间代码的跳转指令对基本块进行划分；上述代码可以翻译为中间代码指令 (简化版）：

1
2
3
4
5
6
7
8
9
10
11
12
(dec,    x,     )
(assign, x,   1 )
(dec,    sum,   )
(assign, sum, 0 )
L0:
(jump if not, x <= 100, L1)
(+=,   sum, x)
(+=,   x  , 1)
(jump, L0 ,  )
L1:
[...]
(call, printf, )

在中间代码中，跳转指令的下一条语句以及跳转指令的目标语句会作为新基本块的首指令，程序的第一条指令也作为基本块的首指令。首指令从自己开始，到下一首指令之间的代码可以划分为一个基本块。因此其分为:

中间代码基本块划分

感兴趣的同学可以往回看看中间代码和原来的代码的划分是怎么样的对应关系，可以从中找到这么划分中间代码的依据。

从基本块到控制流图

控制流图 (Control Flow Graph, CFG) 是一种描述程序执行过程中会执行路径的图。在数据流图中，每节点都是一个基本块，而图的边代表着代码块之间的跳转关系。比如 if-else, while, for 这些语句，在判断完成后，会根据判断结果跳转到不同的分支，执行该分支中的代码，CFG 的边可以描述这种关系。代码分析器可以根据 CFG 判断出代码的执行路径和变量数据的流向。在编译分析中，一般编译器还会加上 ENTRY 节点和 EXIT 节点。如上一节中的代码，我们可以构造出以下数据流图：

CFG

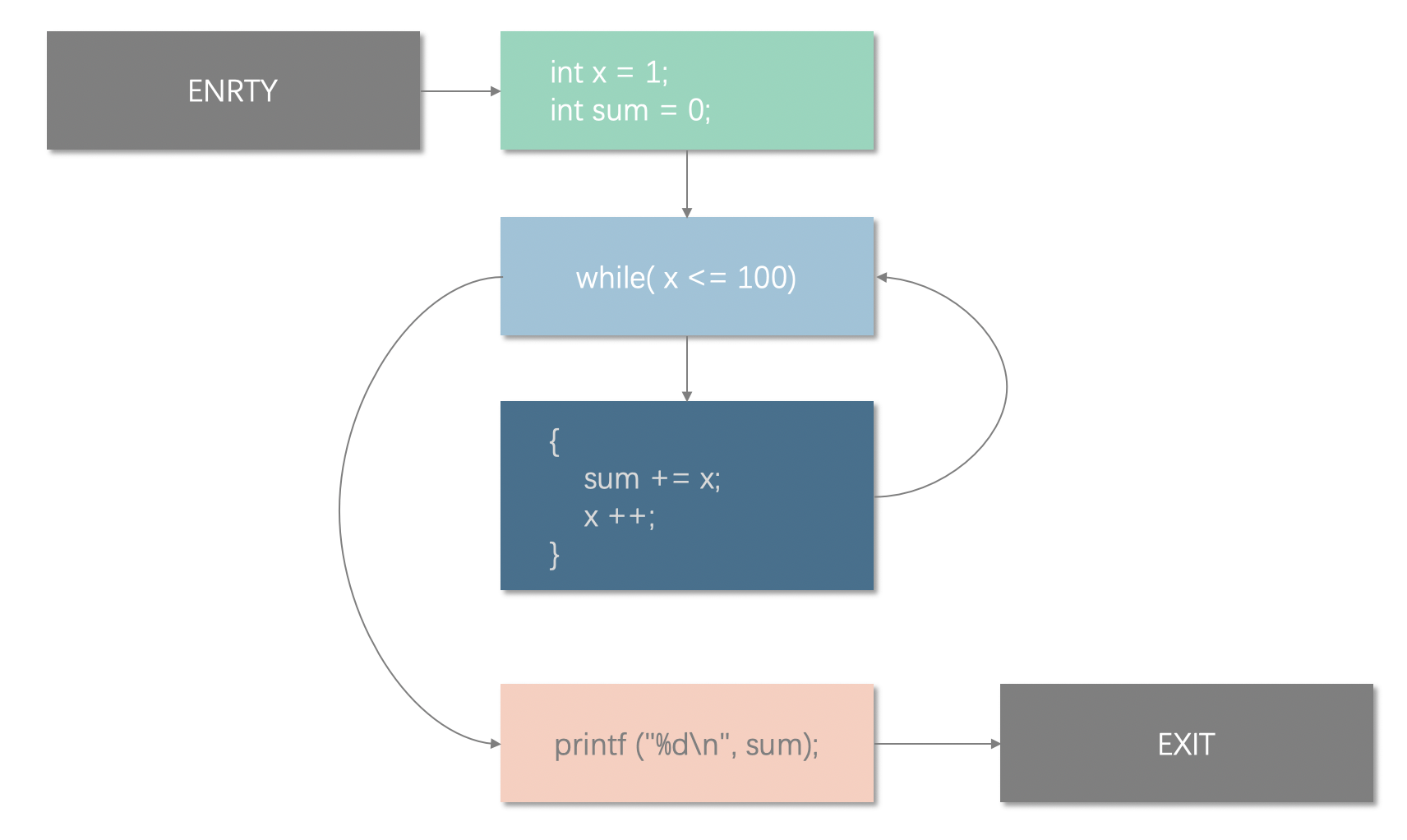
定值？？使用？？？

在讨论具体的数据流分析之前，需要先明确两个非常非常重要的概念

  • 定值 (definition, def): 一般指变量的赋值，一般包括变量声明和初始化、复制、形式参数列表等
  • 使用 (use): 使用变量的值进行运算，一般包括表达式、逻辑判断条件，把变量作为参数传递，返回值等

我们在分析中，一般会把进行了定值和使用操作的变量汇总为两个集合。比如以下代码段中：

1
2
int a = 20;
int b = a + 10;

定值集合和使用集合分别为：

$$
def = { a, b} \
use = { a }
$$

我们定义了 a 和 b 两个整形变量，并且进行了赋值，因此 a 和 b 需要加入到定值集合。 同时我们在给 b 赋值时，使用了 a 的值，此时我们也需要把 a 加入到使用集合。

变量的 “生成” 和 “被杀死”

数据流分析需要分析变量在执行过程中的变化，就需要分析基本块中的定值和使用。在 CFG 中，每个基本块都可能会产生新的变量，或者改写执行路径上前驱节点所定义的值，也就是定值操作。我们可以把定值操作细化两类：

  • 生成 (Genenrate, gen) - 定值的生成，也就是变量的定义、初始化
  • 杀死 (Kill) - 路径上的前驱节点以及给出的定值在本语句中被改写，即前驱节点生成的定值被 “杀” 掉了

一般的，我们可以把在本行或者本基本块代码中新产生的定值集合定义为生成集 $gen[B{i}]$ ，把“被杀死”的定值集合定义为被杀死集合 $kill[B{i}]$。

举个栗子，回到我们前面用的 1 - 100 求和代码，Block A 和 Block C 的代码：

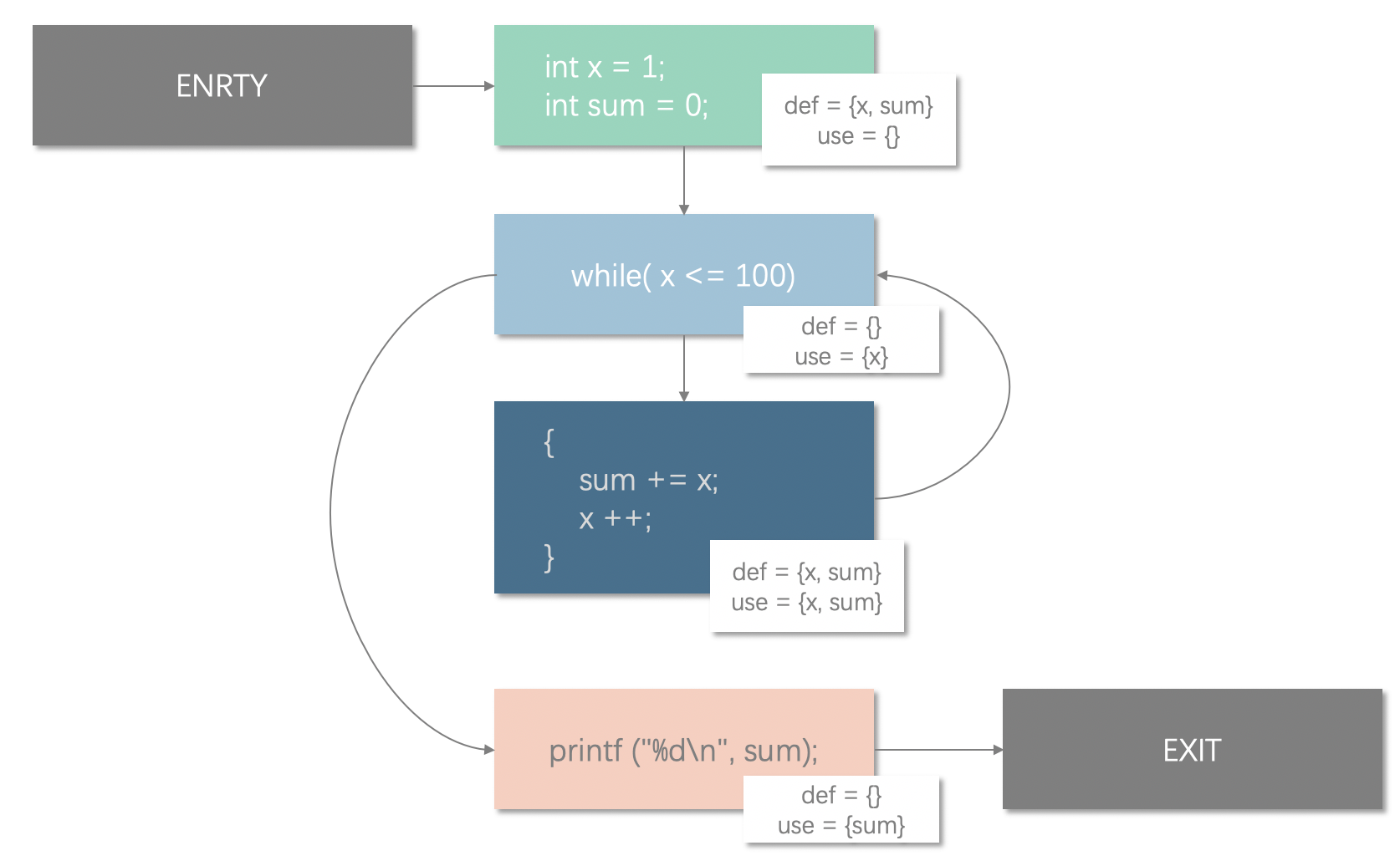
CFG with def-use

在这段代码中，我们可以看到 Block A 中，产生了新的定值 x 和 定值 sum，那么

$$
Gen[A] = {x, sum}
$$

在 Block C 中，sum 和 x 分别改写了在 Block A 中所生成的定值，所以:
$$
Kill[C] = {x, sum}
$$

数据流分析的方式

在控制流图中，每个基本块都会接收到来自其他路径上的前驱节点定值，在经过处理后，会向路径的后继节点发出最新的定值。我们可以规定：

  • $IN[B_{i}]$ 为路径上前驱节点 $B_i$ 发出的到达当前节点的定值集合
  • $OUT[B_{j}]$ 为当前节点向路径上的后继节点 $B_j$ 发出的最新定值集合

由于 CFG 中一个节点可能会从多个节点到达，也可能从当前节点前往不同的节点（如下图），我们需要在指定来自不同节点的定值的合并方式。我们可以把进行定值合并的汇合函数定义为：

$$
\bigcup_{i}^{0..n}IN[i]
$$

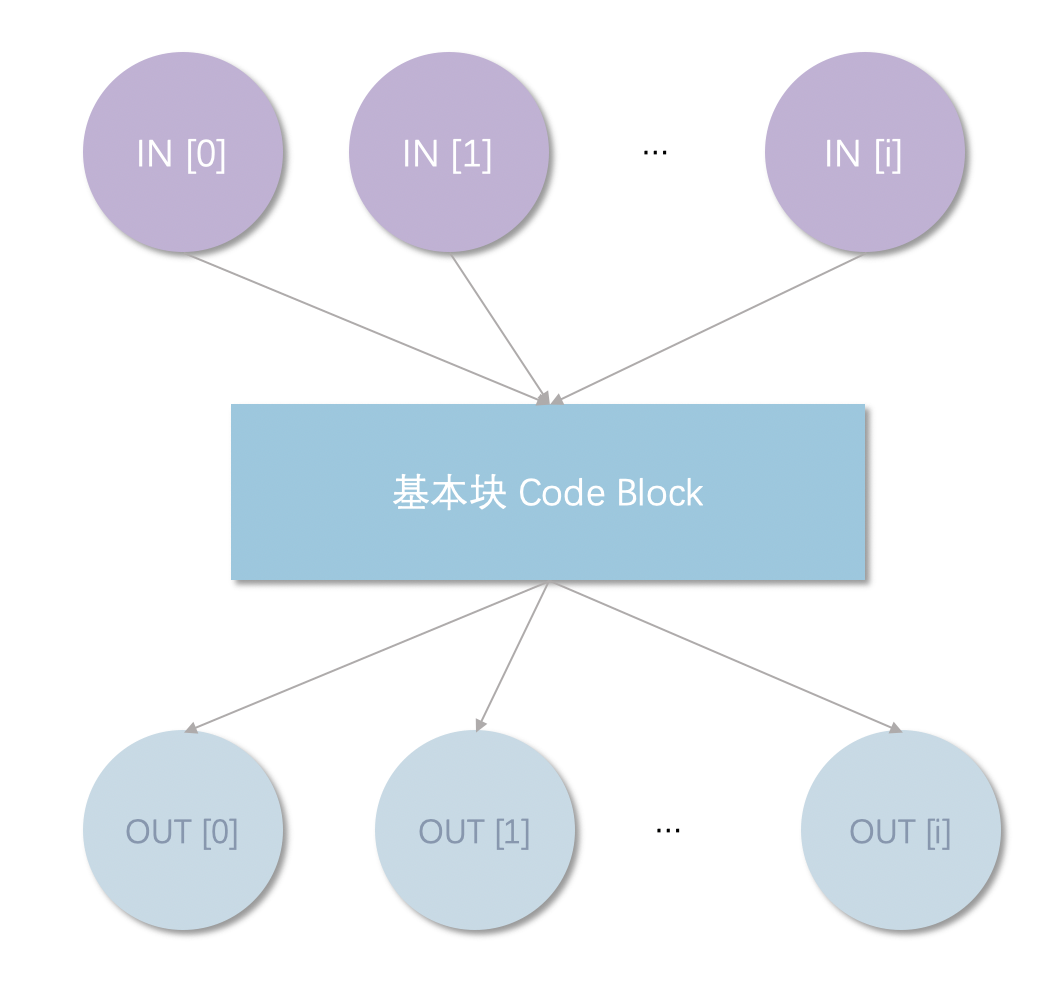
在数据流分析中，汇总后的定值通过节点后，都有可能发生变化，我们把每个节点对定值的操作定义为传递函数 $f_s(x)$。传递函数的传播方向与数据流分析的方向相关。如果数据流采用前向数据分析，那么数据流的信息会沿着执行路径正向传播，节点上的信息来源于路径上的前驱节点，此时传递函数的作用如下：

$$
OUT[B] = f_s(\bigcup_{i}^{0..n}IN[i])
$$

如果数据流采用后向数据分析，那么数据流会沿着执行路径逆向传播，节点上的信息来自于路径上后继节点。此时传递函数为：

$$
IN[B] = f_s(\bigcup_{i}^{0..n}OUT[i])
$$

此外，对于特殊的节点 ENTRY 和 EXIT，我们有

$$
IN[ENTRY] = \emptyset
$$

$$
OUT[EXIT] = IN[EXIT]
$$

到达定值

这一小节是一个例子，阐述我们怎么使用数据流分析计算到达定值。在数据流中，如果一个定值可以从生成的节点，沿着某条路径到达某个节点且在途中未被杀死，我们就称这个定值为到达定值 (Reaching Definition)。我们回到本文最开始的求和程序：

CFG with def-use

我们首先定义我们的分析方向，由于我们要分析的是从定义产生到某个节点，因此分析方向应该是前向分析方法。所以我们可以定义回合函数为：

$$
\bigcup_{i}^{0..n}IN[i] = IN[0] \cup IN[1] \cup … \cup IN[n]
$$

思考一下，如果在基本块中新增了定值，那么在 $OUT$ 中应该要出现，而如果基本块中杀死的定义，我们应该在 $OUT$ 中去除。所以交汇函数应该是：

$$
f_s(B_i) = (\bigcup_{i}^{0..n}IN[i] - Kill[B_{i}])\cup Gen[B_{i}]
$$

我们可以算出（程序计算需要使用迭代的方法）：

Kill Generate
Kill[A] = $\emptyset$; Gen[A] = ${x_{a}, sum_{a}}$
Kill[B] = $\emptyset$; Gen[B] = $\emptyset$
Kill[C] = ${x_{a}, sum_{a}, x_{c}, sum_{c}}$; Gen[C] = ${x_{c}, sum_{c}}$
Kill[D] = $\emptyset$; Gen[D] = $\emptyset$

需要注意的是 Block B 可以从 Block A 和 Block C 到达，因此需要合并两者的 OUT 集合。所以有

Block IN OUT
ENTRY $\emptyset$ $\emptyset$
A $\emptyset$ ${x_{a}, sum_{a}}$
B ${x_{a}, sum_{a}, x_{c}, sum_{c}}$ ${x_{a}, sum_{a}, x_{c}, sum_{c}}$
C ${x_{a}, sum_{a}, x_{c}, sum_{c}}$ ${x_{c}, sum_{c}}$
D ${x_{a}, sum_{a}, x_{c}, sum_{c}}$ ${x_{a}, sum_{a}, x_{c}, sum_{c}}$
EXIT ${x_{a}, sum_{a}, x_{c}, sum_{c}}$ ${x_{a}, sum_{a}, x_{c}, sum_{c}}$

从表中我们可以知道 Block D 的 $sum_{c}$ 来自于 Block C，换言之，$x_{c}$ 是 D 节点的到达定值。

后续

数据流分析可以用于编译器的许多优化场景，或者用于计算机的静态代码检查、静态安全漏洞检查等。未来有机会会再写一些相关的文章进行讨论 （先立个 flag，哈哈）